Redis实现之字典跳跃表

跳跃表
跳跃表是一种有序数据结构,它通过在每个节点中维持多个指向其他节点的指针,从而达到快速访问节点的目的。跳跃表支持平均O(logN)、最坏O(N)的时间复杂度查找,还可以通过顺序性操作来批量处理节点。在大部分情况下,跳跃表的效率可以和平衡树相媲美,并且因为跳跃表的实现比平衡树要来得更简单,所以不少程序都使用跳跃表代替平衡树。Redis使用跳跃表作为有序集合键的底层实现之一,如果一个有序集合包含的元素数量比较多,又或者有序集合中元素的成员是比较长的字符串时,Redis就会使用跳跃表作为有序集合键的底层实现
Redis的ZADD 命令用于将一个或多个成员元素及其分数值加入到有序集当中。如果某个成员已经是有序集的成员,那么更新这个成员的分数值,并通过重新插入这个成员元素,来保证该成员在正确的位置上。分数值可以是整数值或双精度浮点数。如果有序集合 key 不存在,则创建一个空的有序集并执行 ZADD 操作。当 key 存在但不是有序集类型时,返回一个错误
127.0.0.1:6379> ZADD myzset 1 "foo" (integer) 1 127.0.0.1:6379> ZADD myzset 1.5 "bar" (integer) 1 127.0.0.1:6379> ZADD myzset 1 "test" (integer) 1 127.0.0.1:6379> ZADD myzset 2 "hello" (integer) 1 127.0.0.1:6379> ZADD myzset 3 "world" (integer) 1 127.0.0.1:6379> ZRANGE myzset 0 -1 WITHSCORES 1) "foo" 2) "1" 3) "test" 4) "1" 5) "bar" 6) "1.5" 7) "hello" 8) "2" 9) "world" 10) "3" 127.0.0.1:6379> ZCARD myzset (integer) 5
myzset有序集合的所有数据都保存在一个跳跃表里面,其中每个跳跃表节点(node)都保存了一个字符串,所有字符串的按分值从低到高在跳跃表里排序。和链表、字典等数据结构被广泛运用在Redis内部不同,Redis只在两个地方用到跳跃表,一个是实现有序集合键,另一个是集群节点中用作内部数据结构,除此之外,跳跃表只在Redis里没有其他的用途
跳跃表的实现
Redis的跳跃表由zskiplistNode和zskiplist两个结构定义,其中zskiplistNode结构用于表示跳跃表节点,而zskiplist结构则用于保存跳跃表节点的相关信息,比如节点的数量,以及指向表头节点和表尾节点的指针等
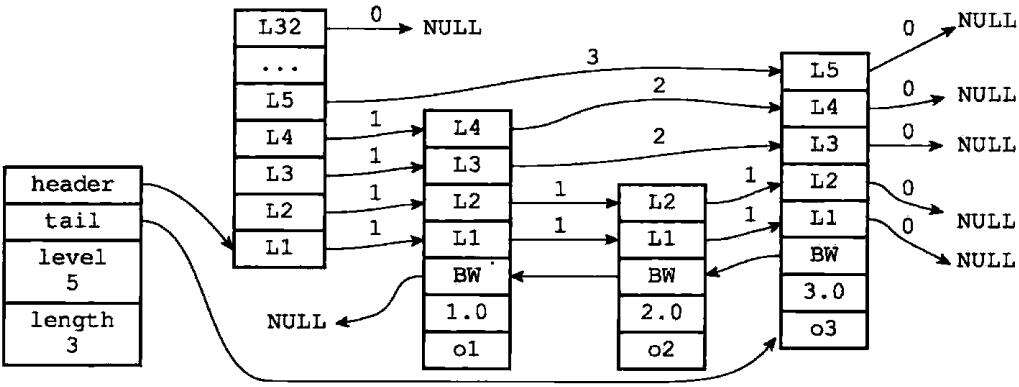
图1-1 一个跳跃表
图1-1展示了一个跳跃表示例,位于图片最左边的是zskiplist结构,该结构包含以下属性:
- header:指向跳跃表的表头节点
- tail:指向跳跃表的表尾节点
- level:记录目前跳跃表内,层数最大的那个节点的层数(表头节点的层数不计算在内)
- length:记录跳跃表的长度,也即是,跳跃表目前包含节点的数量(表头节点不计算在内)
位于zskiplist 结构右方的是四个zskiplistNode结构,该结构包含以下属性:
- 层(level):节点中用 L1 、L2 、L3 等字样标记节点的各个层,L1代表第一层,L2 代表第二层,以此类推。每个层都带有两个属性:前进指针和跨度。前进指针用于访问位于表尾方向的其他节点,而跨度则记录了前进指针所指向节点和当前节点的距离。在上面的图片中,连线上带有数字的箭头就代表前进指针,而那个数字就是跨度。当程序从表头向表尾进行遍历时,访问会沿着层的前进指针进行。
- 后退(backward)指针:节点中用 BW 字样标记节点的后退指针,它指向位于当前节点的前一个节点。后退指针在程序从表尾向表头遍历时使用
- 分值(score):各个节点中的1.0 、2.0 和3.0是节点所保存的分值。在跳跃表中,节点按各自所保存的分值从小到大排列
- 成员对象(obj):各个节点中的o1 、o2 和o3是节点所保存的成员对象
跳跃表节点
redis.h
typedef struct zskiplistNode {
//成员对象
robj *obj;
//分值
double score;
//后退指针
struct zskiplistNode *backward;
//层
struct zskiplistLevel {
//前进指针
struct zskiplistNode *forward;
//跨度
unsigned int span;
} level[];
} zskiplistNode;
层
跳跃表节点的level数组可以包含多个元素,每个元素都包含一个指向其他节点的指针,程序可以通过这些层来加快访问其他节点的速度,一般来说,层的数量越多,访问其他节点的速度就越快。每次创建一个新跳跃表节点的时候,程序都根据幂次定律(power law,越大的数出现的概率越小)随机生成一个介于1和32之间的值作为level数组的大小,这个大小就是层的高度。图1-2分别展示了三个高度为一层、三层和五层的节点,因此C语言的数组索引总是从0开始,所以节点的第一层是level[0],第二层是level[1],以此类推
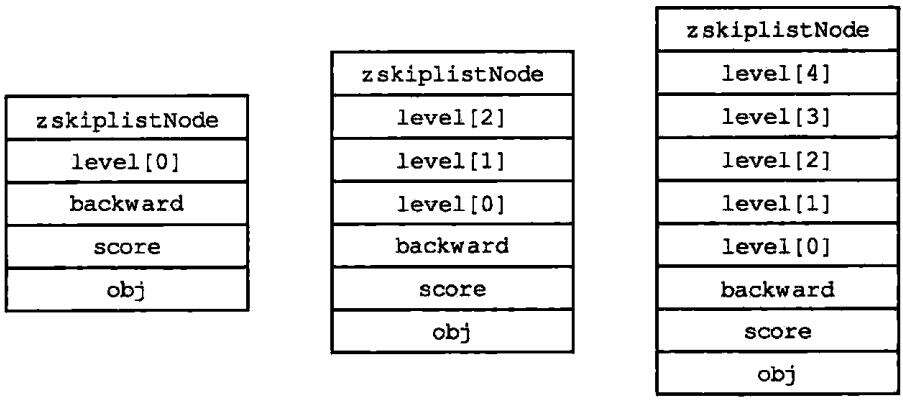
图1-2 带有不同层高的节点
前进指针
每个层都有一个指向表尾方向的前进指针(level[i].forward属性),用于从表头向表尾方向访问节点。图1-3用虚线表示出了程序从表头向表尾方向,遍历跳跃表中所有节点的路径
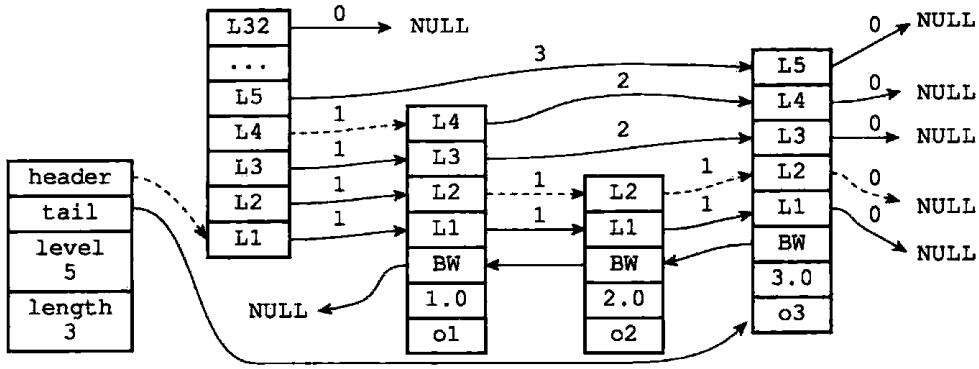
图1-3 遍历整个跳跃表
- 迭代程序首先访问跳跃表的第一个节点(表头),然后从第四层的前进指针移动到表中的第二个节点
- 在第二个节点时,程序沿着第二层的前进指针移动到表中的第三个节点
- 在第三个节点时,程序同样沿着第二层的前进指针移动到表中的第四个节点
- 当程序再次沿着第四个节点的前进指针移动时,碰到一个NULL,程序知道这时已经到达了跳跃表的表尾,于是结束这次遍历
跨度
层的跨度(level[i].span属性)用于记录两个节点之间的距离:
- 两个节点之间的跨度越大,它们相距得就越远
- 指向NULL的所有前进指针的跨度都为0,因为它们没有连向任何节点
初看上去,很容易以为跨度和遍历操作有关,但实际上并不是这样,遍历操作只使用前进指针就可以完成,跨度实际上是用来你计算排位(rank)的:在查找某个节点的过程中,将沿途访问过的所有层的跨度累计起来,得到的结果就是目标节点在跳跃表的排位。举个栗子,图1-4用虚线标记了在跳跃表中查找分值为3.0,成员对象为o3的节点时,沿途经历的层:查找的过程只经过了一层,并且层的跨度为3,所以目标节点在跳跃表中的排位为3
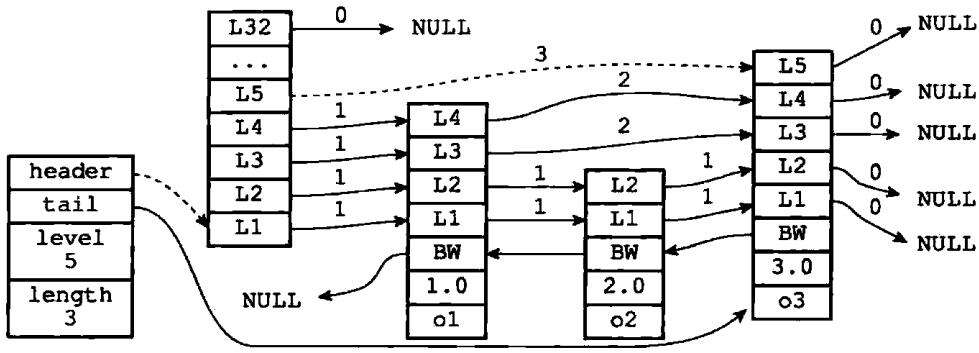
图1-4 计算节点的排位
再举个栗子,图1-5用虚线标记了在跳跃表中查找分值为2.0、成员对象为o2的节点时,沿途经历的层:在查找节点的过程中,程序经过了两个跨度为1的节点,因此可以计算出,目标节点在跳跃表中的排位为2
后退指针
节点的后退指针用于从表尾向表头方向访问节点,跟可以一次跳过多个节点的前进指针不同,因为每个节点只有一个后退指针,所以每次只能后退至前一个节点。图1-6用虚线展示了如果从表尾向表头遍历跳跃表中的所有节点:程序首先通过跳跃表的tail指针访问表尾节点,然后通过后退指针访问倒数第二个节点,之后再沿着后退指针访问倒数第三个节点,再之后遇到指向NULL的后退指针,于是访问结束
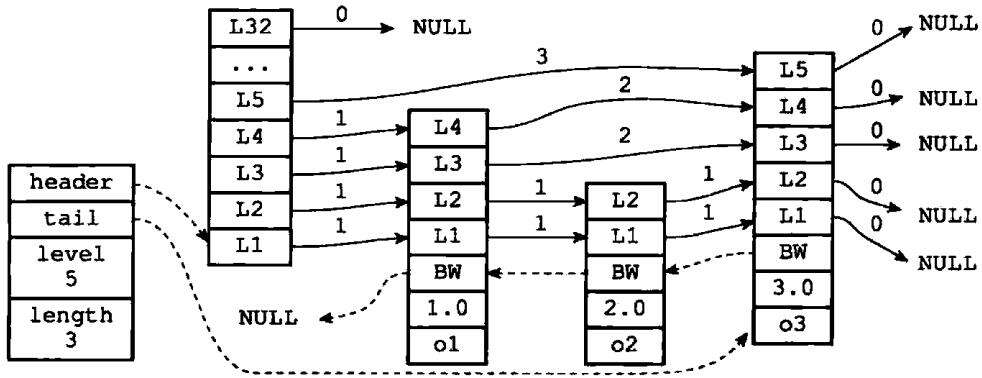
图1-6 从表尾向表头方向遍历跳跃表
分值和成员
节点的分值(score属性)是一个double类型的浮点数,跳跃表中的所有节点都按分值从小到大排序。节点的成员对象(obj属性)是一个指针,它指向一个字符串对象,而字符串对象则保存着一个SDS值。在同一个跳跃表中,各个节点保存的成员对象必须是唯一的,但是多个节点保存的分值却可以是相同的:分值相同的节点将按照成员对象在字典序中的大小来进行排序,成员对象较小的节点会排在前面(靠近表头的地方),而成员对象较大的节点会排在后面(靠近表尾的方向)
举个栗子,在图1-7所示的跳跃表中,三个跳跃表节点都保存了相同的分值10086.0,但保存成员对象o1的节点却排在保存成员对象o2和o3的节点之前,而保存成员对象o2的节点又排在保存成员对象o3的节点之前,由此可见,o1、o2、o3三个成员对象在字典中的排序为o1<=o2<=o3
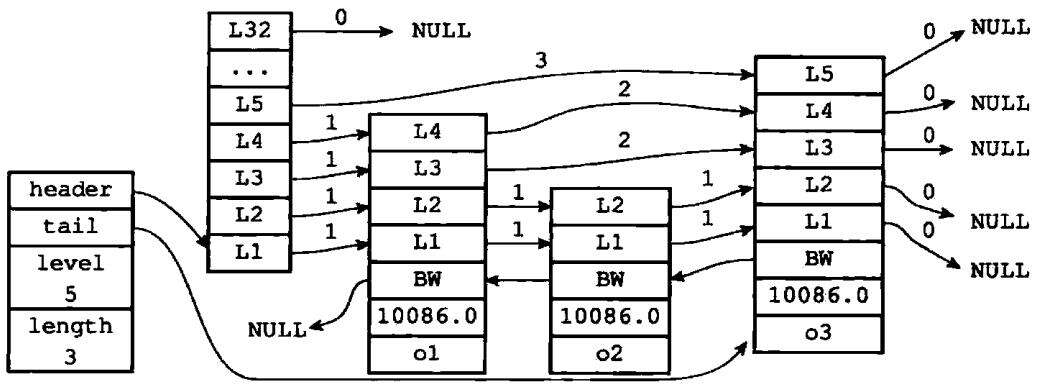
图1-7 三个带有相同分值的跳跃表节点
跳跃表
redis.h
typedef struct zskiplist {
//表头节点和表尾节点
struct zskiplistNode *header, *tail;
//表中节点的数量
unsigned long length;
//表中层数最大的节点的成熟
int level;
} zskiplist;
仅靠多个跳跃表节点就可以组成一个跳跃表,如图1-8所示。
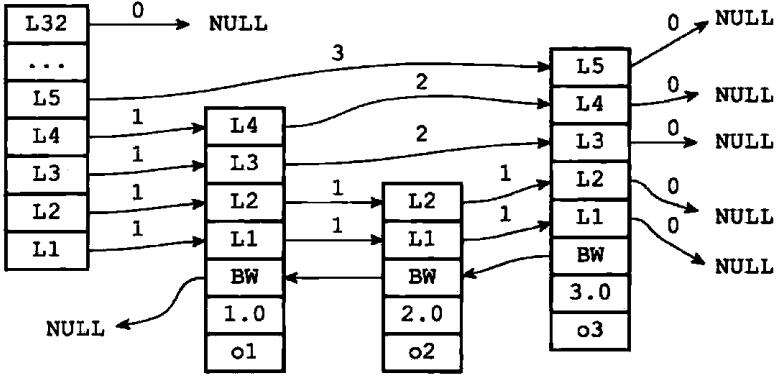
图1-8 由多个跳跃节点组成的跳跃表
但通过使用一个zskiplist结构来持有这些节点,程序可以更方便地对整个跳跃表进行处理,比如快速访问跳跃表的表头节点和表尾节点,或者快速地获取跳跃表节点的数量(即跳跃表长度)等信息,如图1-9所示
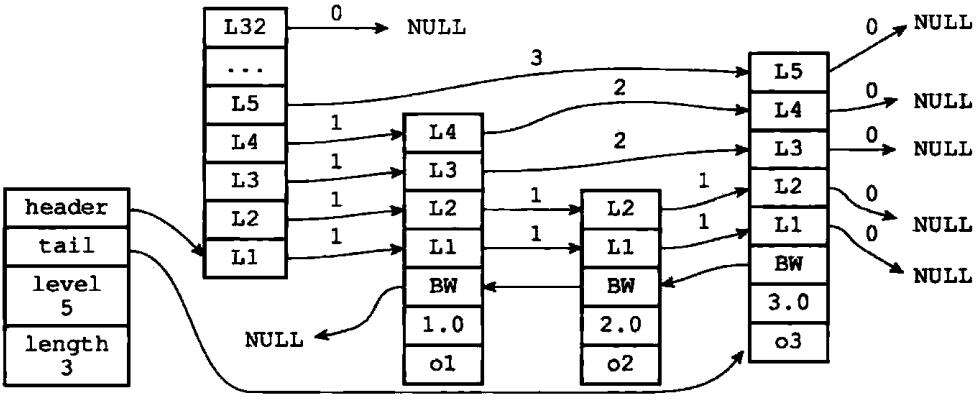
图1-9 带有zskiplist结构的跳跃表
header和tail指针分别指向跳跃表的表头和表尾节点,通过这两个指针,程序定位表头节点和表尾节点的时间复杂度为O(1)。通过使用length属性记录节点的数量,程序获取跳跃表长度的时间复杂度为O(1)。同理,程序可以在O(1)内的时间复杂度通过level属性记录跳跃表中层高最大的那个节点的层数,注意表头节点的层高并不在计算内
跳跃表API
表1-1列出跳跃表的所有操作API
| 函数 | 作用 | 时间复杂度 |
| zslCreate(void) | 创建一个新的跳跃表 | O(1) |
| zslFree(zskiplist *zsl) | 释放给定跳跃表,以及表中包含的所有节点 | O(N),N为跳跃表的长度 |
| zslInsert(zskiplist *zsl, double score, robj *obj) | 将包含给定成员和分值的新节点添加到跳跃表中 | 平均O(logN),最坏O(N),N为跳跃表长度 |
| zslDelete(zskiplist *zsl, double score, robj *obj) | 删除跳跃表中包含给定成员和分值的节点 | 平均O(logN),最坏O(N),N为跳跃表长度 |
| zslGetRank(zskiplist *zsl, double score, robj *o) | 返回包含给定成员和分值的节点在跳跃表中的排位 | 平均O(log N),最坏O(N),N为跳跃表长度 |
| zslGetElementByRank(zskiplist *zsl, unsigned long rank) | 返回跳跃表在给定排位上的节点 | 平均O(logN),最坏O(N),N为跳跃表长度 |
| zslIsInRange(zskiplist *zsl, zrangespec *range) | 给定一个分值范围(range),比如0到15,20到28 ,诸如此类,如果给定的分值范围包含在跳跃表的分值范围之内,那么返回 1,否则返回 0 | 通过跳跃表的表头节点和表尾节点,这个检测可以用O(1)复杂度完成 |
| zslFirstInRange(zskiplist *zsl, zrangespec range) | 给定一个分值范围,返回跳跃表中第一个符合这个范围的节点 | 平均O(logN),最坏O(N)。N为跳跃表长度 |
| zslLastInRange(zskiplist *zsl, zrangespec range) | 给定一个分值范围,返回跳跃表中最后一个符合这个范围的节点 | 平均O(logN),最坏O(N)。N为跳跃表长度 |
| zslDeleteRangeByScore(zskiplist *zsl, zrangespec range, dict *dict) | 给定一个分值范围,删除跳跃表中所有在这个范围之内的节点 | O(N),N为被删除节点数量 |
| zslDeleteRangeByRank(zskiplist *zsl, unsigned int start, unsigned int end, dict *dict) | 给定一个排位范围,删除跳跃表中所有在这个范围之内的节点 | O(N),N为被删除节点数量 |
