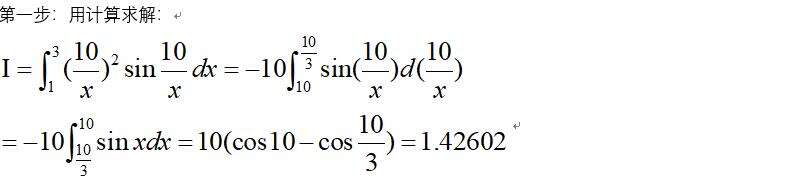C语言实现变步长求积分算法

链接：https://blog.csdn.net/chen_dsir/article/details/71257631  博主详细介绍了复合梯形公式，

链接：https://wenku.baidu.com/view/b300c53deefdc8d376ee3228.html 详细介绍了变步长的目的，以及变换的方式

下面求解如下问题：

1、变步长：

        由于多数情况下，并不知道步长设置为多少合适，所以我们可以设置一个初始步长，求解一次，再把步长变为原来的一半，依次接下去，直到达到我们所需的精度。

2、代码：

#include<stdio.h>
#include<math.h>

#define left 1.0   //左端的值 
#define right 3.0   //右端的值 
#define  precision 0.0001   //定义精度 


double f(double x)
{
	double m=100/(x*x)*sin(10/x);
	return m;
}

int main()
{
	int i;
	int step=100;  //初始化步数
	double stepLength=(right-left)/step; //步长
	double T=f(left)+f(right);   //积分的值 
	for(i=1;i<=step-1;i++) 
	{
		double x=left+i*stepLength;
		T+=2*f(x);
	}
	T=stepLength/2*T;  //符合梯形公式求解结果
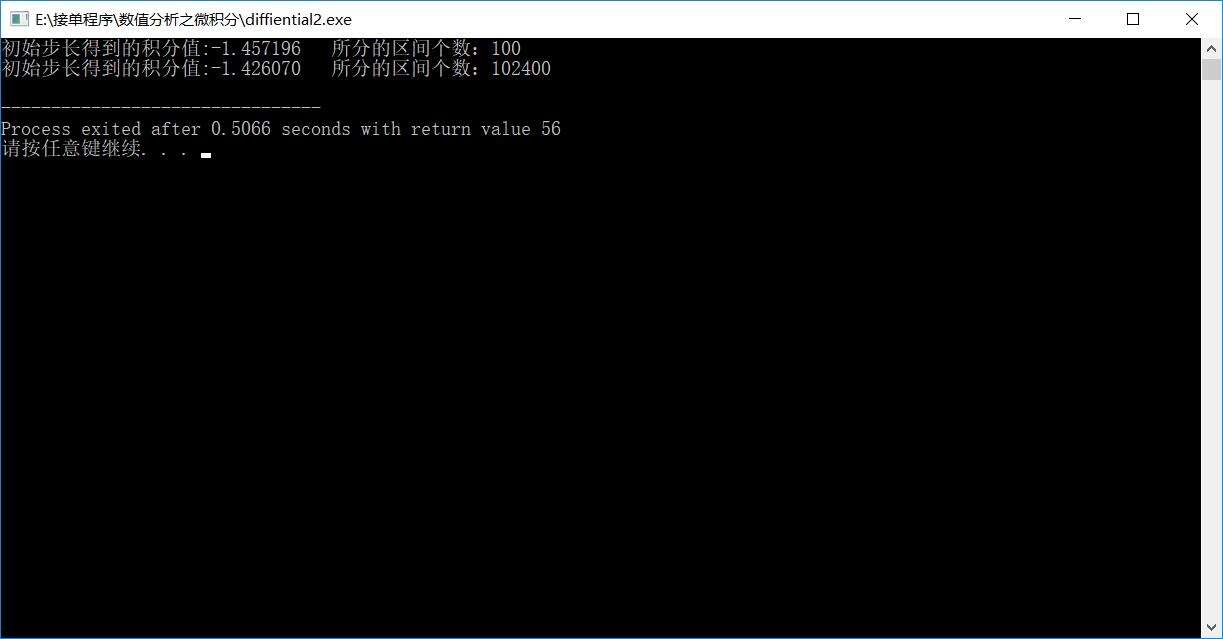
	printf("初始步长得到的积分值:%lf   所分的区间个数：%d\n",T,step);
	//下面改变步长，来细化精度
	double T1=T+100;
	double T2=T;
	double H;      //减小步长后得到的积分值 
	while(fabs(T1-T2)>precision/2) 
	{
		T1=T2;
		step=step*2;
		stepLength=(right-left)/step; 
		H=0;
		for(i=1;i<step;i++)
		{
			H+=2*f(left+stepLength*i);
		}
		H=f(left)+f(right)+H;
		H=H*stepLength/2;     
		T2=(T1+H)/2;    //将上次一的积分结果和减小步长后的积分结果求均值 
		
	}	
	printf("初始步长得到的积分值:%lf   所分的区间个数：%d\n",T2,step);
	
	 
	
}

3、结果：

4、验证：