排序算法（C语言版）

交换类

• 冒泡排序（Bubble Sort） $O\left(n^2\right)$O(n2)

最简单的一种排序算法。先从数组中找到最大值(或最小值)并放到数组最左端(或最右端)，然后在剩下的数字中找到次大值(或次小值)，以此类推，直到数组有序排列。

void BubbleSortPlus(SqList L)
{
    int i, j, t, flag;
    flag = TRUE;

    for(i = 1; i <= L.length - 1 && flag; i++)
        for(j = 1; j <= L.length - 1 - i; j++)
        {
            flag = FALSE;
            if(L.elem[j] > L.elem[j+1])
            {
                t = L.elem[j];
                L.elem[j] = L.elem[j+1];
                L.elem[j+1] = t;
                flag = TRUE;
            }
        }
}

• 快速排序（Quick Sort）$O\left(nlgn\right)$O(nlgn)（平均，最坏情况为冒泡排序）

快速排序的基本思想是：通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，已达到整个序列有序。一趟快速排序的具体过程可描述为：从待排序列中任意选取一个记录(通常选取第一个记录)作为基准值，然后将记录中关键字比它小的记录都安置在它的位置之前，将记录中关键字比它大的记录都安置在它的位置之后。这样，以该基准值为分界线，将待排序列分成的两个子序列。

void QuickSort(SqList L)
{
    QSort(L, 1, LENGTH);
}

void QSort(SqList &L, int low, int high)
{
    int pivotloc;
    if(low < high)
    {
        pivotloc = Partition(L, low, high);
        QSort(L, low, pivotloc - 1);
        QSort(L, pivotloc + 1 , high);
    }
}

int Partition(SqList &L, int low, int high)
{
    L.elem[0] = L.elem[low];

    while(low < high)
    {
        while(low < high && L.elem[high] >= L.elem[0])
        {
            high--;
        }
        L.elem[low] = L.elem[high];
        while(low < high && L.elem[high] <= L.elem[0])
        {
            low++;
        }
        L.elem[high] = L.elem[low];
    }

    L.elem[low] = L.elem[0];

    return low;
}

插入类

• 直接插入排序（Straight Insertion Sort） $O\left(n^2\right)$O(n2)

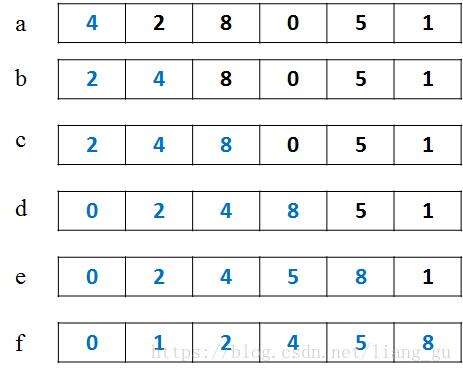
插入排序的基本思想就是将无序序列插入到有序序列中。例如要将数组arr=[4,2,8,0,5,1]排序，可以将4看做是一个有序序列(图中用蓝色标出)，将[2,8,0,5,1]看做一个无序序列。无序序列中2比4小，于是将2插入到4的左边，此时有序序列变成了[2,4]，无序序列变成了[8,0,5,1]。无序序列中8比4大，于是将8插入到4的右边，有序序列变成了[2,4,8],无序序列变成了[0,5,1]。以此类推，最终数组按照从小到大排序。

void InsertSort(SqList L)
{
    int i, j;
    
    for(i = 2; i <= L.length; i++)
    {
        if(L.elem[i] < L.elem[i-1])
        {
            L.elem[0] = L.elem[i];
            L.elem[i] = L.elem[i-1];
            for(j = i - 2; L.elem[0] < L.elem[j]; j--)
            {
                L.elem[j+1] = L.elem[j];
            }

            L.elem[j+1] = L.elem[0];
        }
    }
}

• 希尔排序（Shell Sort） $O\left(n^{\frac{3}{2}}\right)$O(n23?)(较好情况）

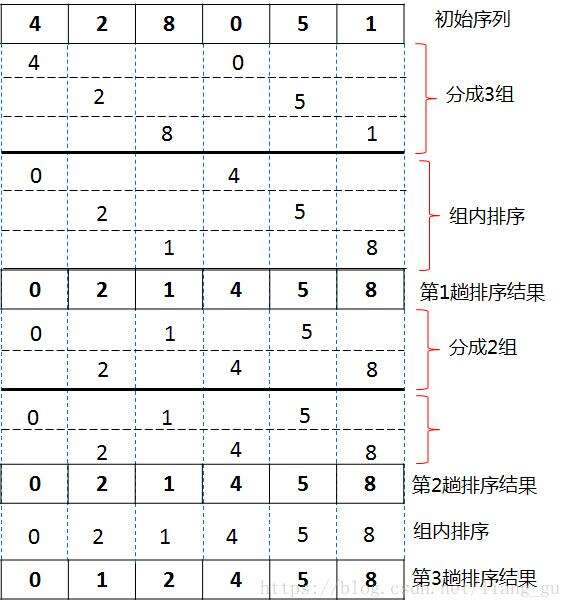
希尔排序(Shell Sort)在插入排序算法的基础上进行了改进，算法的时间复杂度与前面几种算法相比有较大的改进。其算法的基本思想是：先将待排记录序列分割成为若干子序列分别进行插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行一次直接插入排序。

void ShellSort(SqList L)
{
    int i, j, dk = L.length;
    
    do
    {
        dk = dk / 3 + 1;
        for(i = dk + 1; i <= L.length; i++)
        {
            if(L.elem[i] < L.elem[i-dk])
            {
                count1++;
                L.elem[0] = L.elem[i];  //L.elem[0]不是哨兵
                L.elem[i] = L.elem[i-dk];
                for(j = i - 2 * dk; j > 0 && L.elem[0] < L.elem[j]; j--)
                {
                    L.elem[j+dk] = L.elem[j];
                }

                L.elem[j+dk] = L.elem[0];

            }
        }
    }while(dk > 1);
}

选择类

• 简单选择排序（Simple Selection Sort） $O\left(n^2\right)$O(n2)

每一趟在n-i+1(i=1,2,…,n-1)个记录中选取关键字最小的记录作为有序序列中第i个记录。

void InsertSort(SqList L)
{
    int i, j;

    for(i = 2; i <= L.length; i++)
    {
        if(L.elem[i] < L.elem[i-1])
        {
            L.elem[0] = L.elem[i];
            L.elem[i] = L.elem[i-1];
            for(j = i - 2; L.elem[0] < L.elem[j]; j--)
            {
                L.elem[j+1] = L.elem[j];
            }

            L.elem[j+1] = L.elem[0];
        }
    }
}

• 堆排序（Heap Sort） $O\left(nlgn\right)$O(nlgn)

堆的定义如下: n个元素的序列{k1, k2, … , kn}当且仅当满足一下条件时，称之为堆。
$\{\begin{array}{ccc}{k}_i?k_{2i}& or& k_i?k_{2i}\\ k_i?k_{2i+1}& & k_i?k_{2i+1}\\ & (i=1,2,\mathrm{.}\mathrm{.}\mathrm{.},?n\mathrm{/}2?)\end{array}$??????ki??k2i?ki??k2i+1??or(i=1,2,...,?n/2?)?ki??k2i?ki??k2i+1??
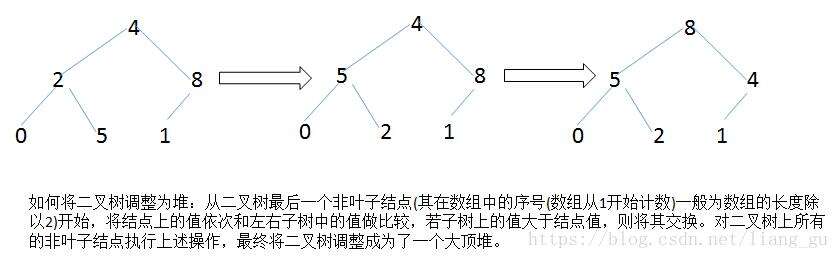
堆排序(Heap Sort)是利用堆进行排序的方法。其基本思想为：将待排序列构造成一个大顶堆(或小顶堆)，整个序列的最大值(或最小值)就是堆顶的根结点，将根节点的值和堆数组的末尾元素交换，此时末尾元素就是最大值(或最小值)，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次大值(或次小值)，如此反复执行，最终得到一个有序序列。

void HeapSort(SqList L)
{
    int i, t;

    for(i = L.length / 2; i > 0; i--) //建堆
        HeapAdjust(L, i, L.length);

    for(i = L.length; i > 1; i--)
    {
        t = L.elem[1];
        L.elem[1] = L.elem[i];
        L.elem[i] = t;

        HeapAdjust(L, 1, i - 1);
    }
}

void HeapAdjust(SqList &L, int s, int m)
{
    int rc = L.elem[s], j;

    for(j = 2 * s; j <= m; j *= 2)
    {
        if(j < m && L.elem[j] < L.elem[j+1])
            j++;
        L.elem[s] = L.elem[j];
        s = j;
    }
    L.elem[s] = rc;
}

归并类

• 归并排序（Merge Sort） $O\left(nlgn\right)$O(nlgn)（平均、最佳）

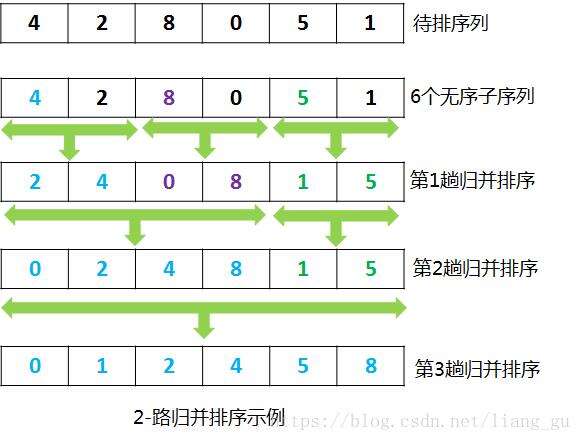
“归并”的含义是将两个或两个以上的有序序列组合成一个新的有序表。假设初始序列含有n个记录，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到$?n\mathrm{/}2?$?n/2?个长度为2(或者是1)的有序子序列，再两两归并。如此重复，直到得到一个长度为n的有序序列为止。这种排序方法称为2-路归并排序。

void MergeSort(SqList L)
{
    MSort(L, 1, L.length);
}

void MSort(SqList &L, int low, int high)
{
    int mid;

    if(low < high)
    {
        mid = (low + high) / 2;
        MSort(L, low, mid);
        MSort(L, mid + 1, high);
        Merge(L, low, mid, high);
    }
}

void Merge(SqList &L, int low, int mid, int high)
{
    int m, n, i, j;
    m = mid - low + 1;
    n = high - mid;
    int M[m], N[n];

    for(i = 0; i < m; i++)
        M[i] = L.elem[low+i];
    for(j = 0; j < n; j++)
        N[j] = L.elem[mid+j+1];


    i = j = 0;

    while(i < m && j < n)
    {
        if(M[i] <= N[j])
            L.elem[low++] = M[i++];
        else
            L.elem[low++] = N[j++];
    }

    while(i < m)
    {
        L.elem[low++] = M[i++];
    }

    while(j < n)
    {
        L.elem[low++] = N[j++];
    }
}